衍射的博客

记录学习中的点点滴滴

0%

[ICSE 2021] MicroHECL: High-Efficient Root Cause Localization in Large-Scale Microservice Systems

发表于 更新于 分类于
本文字数： 4k 阅读时长 ≈ 7 分钟

题目：MicroHECL: High-Efficient Root Cause Localization in Large-Scale Microservice Systems

来源：ICSE 2021

作者：复旦大学CodeWisdom团队，阿里云

摘要

微服务系统的可用性问题直接影响了业务的运行，这些问题通常由各种各样的故障类型以及服务间故障的传播造成。如何设计精准且高效定位故障根因的方法成为了一个重大挑战。然而，现有基于服务调用图的方法在异常检测的准确率和图游走的效率上存在不足。本文提出了一种高效的根因定位方法MicroHECL，通过如下步骤定位故障根因：

  • 动态构建一段时间窗口内的服务调用图
  • 对不同异常类型进行个性化异常检测
  • 对不同异常类型分析异常传播链路，通过剪枝提高效率

背景

工业微服务系统包含大量的微服务（e.g., alibaba有3000个微服务，300个子系统）。一个服务都可能运行在成百上千个容器中，并时常动态创建和销毁。服务之间也存在复杂的调用关系（同步、异步）。

微服务系统可用性问题可能由不同类型的异常引起，每种异常都由一组指标表示。异常可能源自服务并沿服务调用传播，最终导致可用性问题。文章具体关注三种故障类型（就是谷歌提到的几种黄金指标）：

  • 性能异常（Performance Anomaly）
  • 可靠性异常（Reliability Anomaly）
  • 流量异常（Traffic Anomaly）

MicroHECL 概述

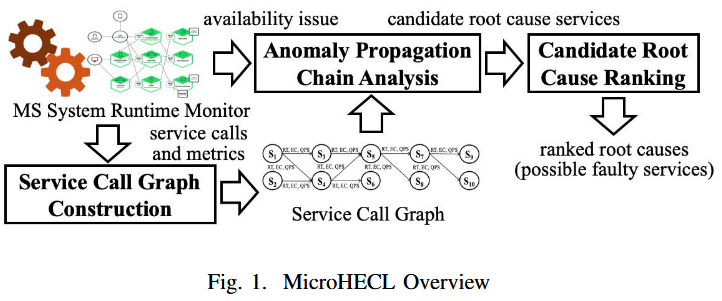
MicroHECL支持三种故障类型的检测和诊断：性能异常、可靠性异常和流量异常。最终输出候选的故障根因服务排名。

服务调用图构建

当MicroHECL检测到异常后（3-sigma），会启动根因分析流程，首先就是构建过去30min内的服务依赖图（service call graph）。图上的节点就是每一个微服务；图上的边代表服务之间的调用关系，比如\(S_i \to S_j\)代表微服务\(S_i\)调用了微服务\(S_j\)；节点上具有一些属性：响应时间（RT），错误数量（EC）以及每秒请求量（QPS）。

异常传播链分析

检测到异常的微服务并不一定是故障根因，但是故障根因一般在这个微服务的上游或者下游。异常传播链分析的目的是筛选初始异常服务中可能的异常传播链来识别一组候选根本原因服务。整个过程由以下几步组成：

  • 分析入口服务（即最初汇报异常的微服务，后面会混用）
  • 异常传播链扩展
  • 根因排序

分析入口服务

文章首先根据经验定义了三种故障类型的传播方向：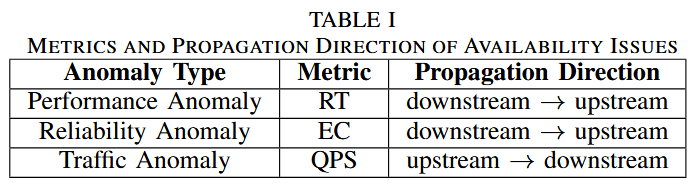

性能异常和可靠性异常的传播方向很好理解，因为上游服务的响应时间和状态码受下游服务影响。流量异常的传播方向是从上游到下游，原因是【笔者自己的理解】上游服务发生了故障（比如网络拥塞），那么发送到下游的流量会大幅减少，所以下游服务会出现QPS急剧减少的异常。这个结论也可以在ImpactTracer1中找到。

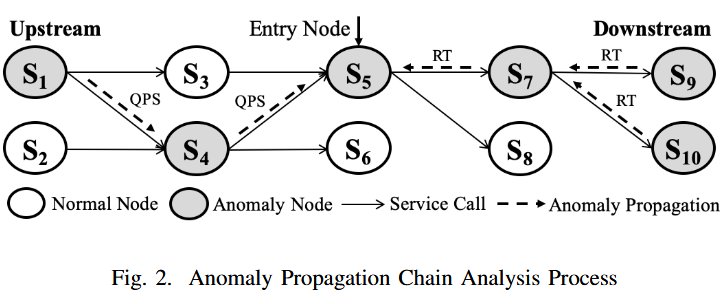
有了故障的传播方向，文章从入口服务开始，向邻居节点不断扩展分析。如图Fig. 2所示，整个过程描述如下： > 1. 将入口服务\(S_5\)纳入异常传播链 > 2. 异常检测。检测\(S_5\)的邻居节点\(S_4\)和\(S_7\)的异常类型 > 3. 确认\(S_4\)的异常类型为Traffic Anomaly，\(S_7\)的异常类型为Performance Anomaly > 4. 检测是否符合传播方向（\(S_4\)是否是\(S_5\)的上游，\(S_7\)是否是\(S_5\)的下游） > 5. 符合，将\(S_4\)和\(S_7\)添加到异常传播链 > 6. 从\(S_4\)和\(S_7\)出发，对邻居节点重复上述步骤

以上过程其实就是故障的溯源，图中的箭头可以看作故障的传播路径。过程中涉及的异常检测在3.3节会提到。

异常传播链扩展

过程与3.2.1中描述的扩展过程一致。对于每个检测到的上游/下游异常节点，将其添加到异常传播链中。当无法向链中添加更多节点时，异常传播链的扩展结束。比如Fig. 2对于\(S_4\)方向的传播分析，以\(S_1\)结束；对于\(S_7\)方向的传播分析，以\(S_9\)和\(S_{10}\)结束。

候选根因定位

本文选择异常传播链的末端服务作为候选根因，比如Fig. 2中的候选根因服务为\(S_1\)，\(S_9\)和\(S_{10}\)。那么如何排名呢？

  • 选取入口服务过去60min的业务指标 \(X\)
  • 选取候选根因服务过去60分钟的质量指标（RT, EC or QPS）\(Y\)
  • 计算两者之间的皮尔逊相关系数：

\[ P(X, Y)=\frac{\sum_{i=1}^n{(X_i-\overline{X})(Y_i-\overline{Y})}}{\sqrt{\sum_{i=1}^n{(X_i-\overline{X})^2}\sum_{i=1}^n{(Y_i-\overline{Y})^2}}} \]

皮尔逊相关系数范围为[-1,1]，绝对值越接近1则表明相关性越大。所以，根因则根据皮尔逊相关系数的绝对值来排序。

服务异常检测

这篇文章的重点应该是放在了如何设计精准的异常检测上。不同于以往的方法只使用一种异常检测手段，本文对三种故障类型（Performance Anomaly，Reliability Anomaly，Traffic Anomaly）分别设计了异常检测方法。

这三种方法分别对应三种指标：响应时间（RT），错误数量（EC）以及每秒请求量（QPS），以下是阿里巴巴监控系统中获取的异常案例：

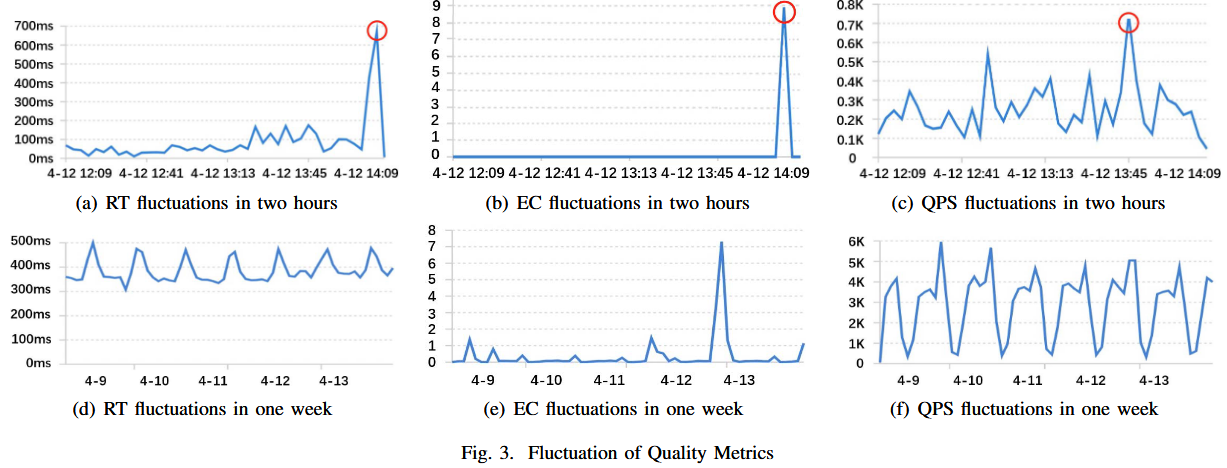
性能异常检测

在RT的异常检测中，需要考虑RT可能存在的周期性（如Fig. 3 (d)）所示，简单的使用3-sigma方法会将这种正常周期波动视为异常。所以不仅需要考虑当前期间的质量指标，还需要考虑前一天和前一周同一天的质量指标。

本文使用OC-SVM训练异常检测模型，OC-SVM是一种常用的无监督机器学习模型，常用于异常检测和分类。文章为RT构建了以下4种特征：

  • 当前检测窗口中RT的值大于给定比较时间窗口内RT的最大值的数量。
  • 当前检测窗口中RT的最大值与给定比较时间窗口内的RT最大值的差值。
  • 当前检测时间窗口中超过给定比较时间窗口中RT滑动平均值最大值的数量。
  • 当前检测窗口中RT的平均值与给定时间窗口内RT的滑动平均值的最大值的比值。

其中，当前检测窗口大小为10min，给定比较时间窗口有3种：①过去一小时、②前一天同一小时、③前一周同一天的同一小时。（如果数据保存没那么完善和严格的话，笔者认为定义一段正常时间为比较窗口应该也是可以接受的）。所以一共有3*4=12种特征。

对于模型训练和验证，文章拿10000样本作为训练集，600个正负比例1:1的样本作为测试集。

可靠性异常检测

这里提到EC大多时候都是0（Fig.2 (b,c)），偶尔会出现少许波动，但很快会恢复（比如断路器打开时EC升高，关闭后EC降低），也没有周期性，如果用性能异常的模型，则会出现大量误报（少许波动都会算进去）。

所以，文章采用随机森林（Random Forest，RF）来分类，文章为EC构建了以下5种特征：

  • 计算最近一小时的EC和前一天同一时间段的EC的增量；使用3-Sigma规则识别当前检测窗口中可能存在的增量异常值；如果存在，则返回异常值的平均值作为特征值，否则返回0。
  • 计算最近一小时内EC值和每一个值的前一分钟EC值的增量；使用3-Sigma规则识别当前检测窗口中可能存在的增量异常值；如果存在，则返回异常值的平均值作为特征值，否则返回0。
  • 检测窗口内的平均RT是否大于设定的阈值（例如，在本文的线上系统中，阈值设置为50ms）
  • 检测窗口内最大错误率（EC/sum(QPS)）。
  • 检测窗口内RT和EC的皮尔逊相关系数

其中，当前检测窗口大小为10min，对于模型训练和验证，文章拿1000样本作为训练集（有标签，正负比1:3），400个正负比例5:3的样本作为测试集。

流量异常检测

QPS大多满足正态分布（Fig.2 (c,f)），所以直接采用3-sigma进行检测。 > 这里笔者有小小的疑问，QPS真的满足正态分布吗？在系统那边的文章，许多流量都是以泊松分布注入的

其中，当前检测窗口大小为10min，选择过去1h计算均值和标准差。3-sigma的均值和方差选择。为了进一步消除误报，还需要检测初始异常服务的QPS和业务指标（就是入口服务被异常检测的指标）的皮尔逊系数，如果大于0.9，则报告流量异常。

剪枝

为了提高MicroHECL的异常回溯效率，需要控制指数增长的异常传播链分支数量，因为不断地进行异常检测也是非常耗时的。

核心思想：异常传播链中的两个连续服务调用的相应质量指标应该具有相似变化趋势

例子：Fig. 2中的 \(S_1 \to S_4\) 和 \(S_4 \to S_5\) 都是Traffic Anomaly 的传播路径，如果\(S_1 \to S_4\) 的 QPS 和 \(S_4 \to S_5\) 的 QPS 没有相似的趋势（即皮尔逊相关系数<0.7），则需要剪掉\(S_1 \to S_4\)，那么\(S_4\)就取代\(S_1\)变成了候选根因。

这里的检测窗口选取的过去60min。剪枝操作执行在异常节点加入异常调用链之前。

总结

文章思路挺好的，有理有据，方法朴实有效。写作的顺序不是传统的总分形式，首先就把整体流程讲完了，然后拿出异常检测和剪枝单独讲，初看有点不适应。

参考文献

[1] Xie R, Yang J, Li J, et al. ImpactTracer: Root Cause Localization in Microservices Based on Fault Propagation Modeling, (DATE), 2023. https://ieeexplore.ieee.org/abstract/document/10137078/