衍射的博客

记录学习中的点点滴滴

0%

[TSC 2024] Diagnosing Performance Issues for Large-Scale Microservice Systems with Heterogeneous Graph

发表于 更新于 分类于
本文字数： 4.4k 阅读时长 ≈ 8 分钟

题目：Diagnosing Performance Issues for Large-Scale Microservice Systems with Heterogeneous Graph

来源：TSC 2024

作者：南开大学AIOps@NKU团队，清华大学Netman实验室

摘要

微服务系统的可用性对于业务运营和企业声誉至关重要。然而，微服务系统的动态性和复杂性给大规模微服务系统的性能问题诊断带来了重大挑战。文章分析了腾讯性能故障的真实案例后，发现故障传播的因果关系与服务之间的调用关系不一致，所以之前基于调用关系的根因定位方法准确率不高。文章提出适用于大规模微服务系统的性能问题诊断方法，MicroDig，步骤如下：

  • 基于调用和微服务之间的因果关系构建异构传播图
  • 采样面向异构的随机游走算法进行根因服务定位

MicroDig在腾讯、Train-Ticket、银行三个数据集上能实现至少85%的top-3 accuracy。

背景

随着微服务系统的快速演变和规模扩张，微服务自身固有的动态性和复杂性给系统的可靠性维护带来了挑战。当微服务系统发生性能异常时，需要及时定位到根因服务，并把问题工单发给对应微服务的团队。然而，由于微服务数量太过庞大（Alibaba有超过30000服务），并且服务之间交互复杂，性能异常在服务之间进行传播，导致大量服务同时异常，进而使得人工诊断变得耗时耗力。

有许多现有工作基于trace来进行根因分析。trace记录了每次请求的调用路径以及相关性能表现，然而，海量的traces会带来极大的存储开销（eBay每天产生150 billion的traces）。所以，越来越多的公司只保留两个服务之间的端到端聚合调用（end-to-end aggregated calls）。

有些工作已经使用了aggregated call（这里指的是Codewisdom团队的GMTA1），采取模式匹配的方式进行根因定位，但需要非常充足的历史故障数据，这在现实场景中很难实现；也有一些工作基于因果图进行根因定位，他们的因果挖掘算法有极高的计算成本，并且准确率较低。

注：aggregated call在GMTA中提到过，应该就是一段时间（比如1 min）内trace的聚合：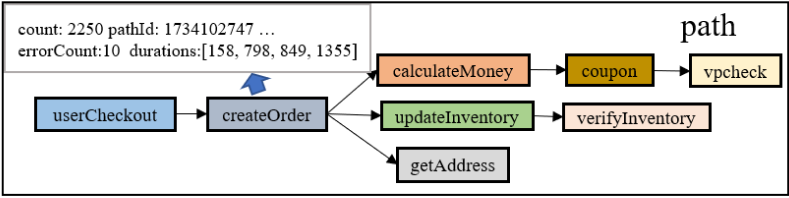

文章提出的MicroDig的核心思想是：调用关系不等于因果关系（在动机中有具体说明），于是在故障诊断前先构造因果图（节点是微服务和调用）。 【从相关工作的分析到方法的提出有点衔接生硬，可能是因为因果方面的分析放到了动机的原因】

动机

调用关系≠异常传播的因果关系

文章举了一个例子来说明这个观点：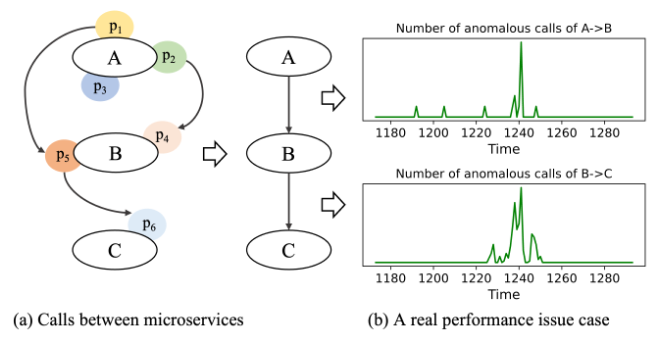

\(A \to B \to C\) 的异常次数急剧增加，如果仅仅根据调用关系去分析异常传播，那么根因是\(C\)，然而，操作员却没有在\(C\)中发现有意义的故障报告。因为 \(B\) 已经用尽了文件描述符，无法建立与 \(C\) 的新连接，所以\(B \to C\)有大量的异常出现。所以根因是\(B\)不是\(C\)，这与调用关系的回溯是违背的。文章提到腾讯有35%的性能问题不能仅仅依靠调用关系回溯解决。

所以异常的被调用服务不一定是根因，调用方和被调用方都有可能是根因

异构传播图

由3.1可知，仅仅从调用关系分析异常传播是不够的，所以本文提出了一种异构传播图（heterogeneous propagation graph）来描述故障传播的因果关系：

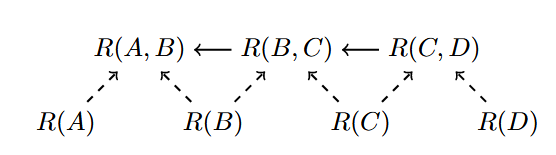
  • 如上图所示，\(R(A,B)\) 代表\(A \to B\)的异常率（anomaly rate），\(R(A)\) 代表服务\(A\) 本身的异常率。注意，服务本身的异常率，如\(R(A)\)，在这个工作中是不可观测的；边的异常率，如\(R(A,B)\)，是可以被观测的。

  • 因为3.1中展示了调用方和被调用方均可能贡献异常，所以每个服务都应该有一条指向调用边的因果线（比如\(R(A) \to R(A,B)\)）。

  • 文章添加了一些假设：①服务之间是独立的，比如\(R(A)\)和\(R(B)\)是独立的【这个假设有点不太符合现实】，②没有交集的两条调用边是独立的，比如\(R(A,B)\)和\(R(C,D)\)

根据作者的设计，这里应该就能看到\(R(B,C)\)是受\(R(B)\)和\(R(C)\)影响的了，从某种意义上给3.1的问题提供了思路。

MicroDig 架构

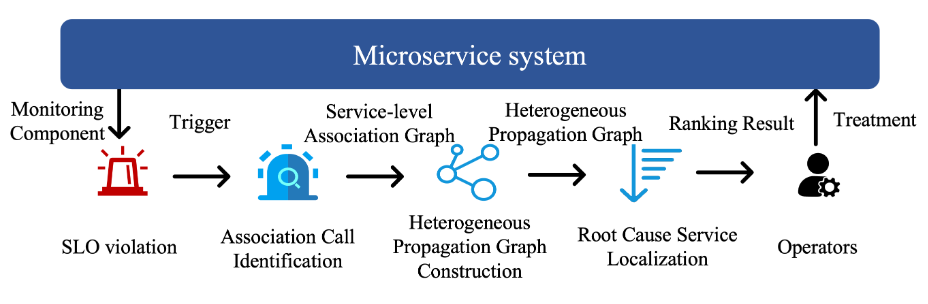
可以看到MicroDig分为几个部分： 1. 性能监控 (Monitoring) 2. 相关调用的识别 (Association Call Identification) 3. 异构传播图的构建 (Heterogeneous Propagation Graph Construction) 4. 根因定位 (Root Cause Localization)

Association Call Identification

对于大规模微服务系统，如果直接构造调用图，那么图中会包含大量与故障不相关的调用边。所以需要对边进行筛选。

构造port-level 异常子图

文章首先构造 port-level 异常子图，port-level即接口级别，图中的节点都是接口， 具体步骤如下：

  1. 构造 port-level 调用图（为什么选用port-level）
  2. 在调用图上进行 宽度优先搜索，对于被遍历的边，采用3-sigma 异常检测 对边的异常率或者超时率进行检测，将异常边保留下来，就得到port-level异常子图

为什么先构造port-level异常子图，而不是直接构造service-level异常子图？因为一个service包含太多port，聚合后一些异常port的表现可能被其他正常port掩盖。

构造service-level 异常子图

聚合构造好的port-level异常子图，即把同一个服务的port节点合并为一个service节点，就得到了service-level异常子图。对于服务\(S\)和\(S'\)，定义\(F(p,p')\)和\(N(p,p')\)分别为其中port-level边\(p \to p'\)的异常调用数和总调用数，那么时间点\(t\)的\(S \to S'\)的异常率\(R_t(S, S')\)为：

\[ R_t(S, S')=\frac{\sum_{p\in S, p' \in S'}F_t(p,p')}{\sum_{p\in S, p' \in S'}N_t(p,p')} \]

整个过程如图(a) (b)所示 ：

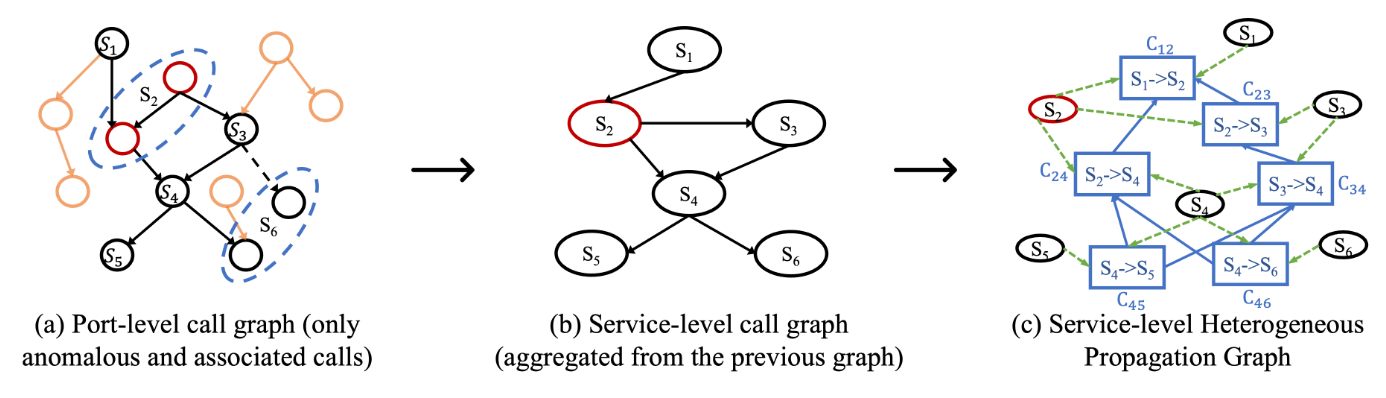
构造 Heterogeneous Propagation Graph

3.1 中提到调用关系≠故障传播的因果关系，所以service-level异常子图也不能直接用于根因定位，需要进一步构建Heterogeneous Propagation Graph （HPG）：

原理很简单： 1. 设置service节点：把service-level异常子图的所有服务加入到 HPG 2. 设置call节点：对于每个服务\(S\)，将\(S\)的出边和入边作为节点加入HPG 3. call节点和service节点的关系：对于每个call节点（\(S \to S'\)），设置 \(S \to (S \to S')\)，\((S \to S') \to S'\) 4. call节点和call节点的关系：对于每个服务\(S\)，设置：出边 \(\to\) 入边

根因服务定位

异构传播图（HPG）有两种节点（service，call）和两种边（service \(\to\) call, call \(\to\) call）。本文采取针对异构图的随机游走算法来定位根因：

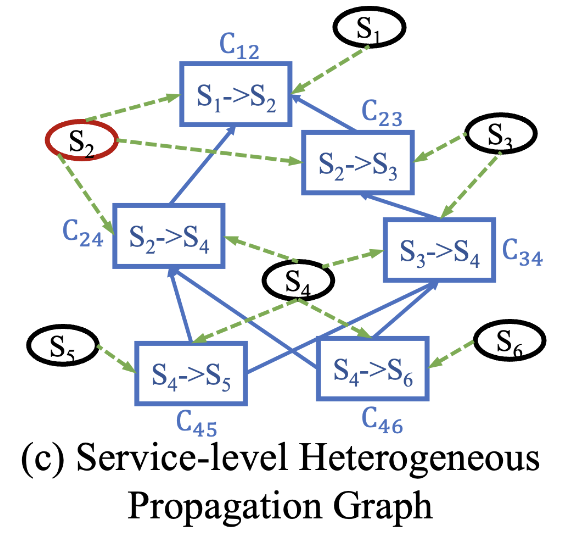
转移权重

随机游走的核心是定义不同边的游走权重：

  1. 对于call \(\to\) call：比如\(C_{23} \to C_{12}\)，通过计算这两个调用的异常率数组之间的相关系数来决定游走权重。
  2. 对于service \(\to\) call：比如\(S_1 \to C_{12}\)

    • 首先计算service的异常程度，定义\(\mathbb{S}_U\)和\(\mathbb{S}_D\)分别表示服务\(S\)的上游服务集合和下游服务集合，服务\(S\)的异常程度\(\alpha_S\)可以表示为： \[ \alpha_S = \frac{|\{S'|S'\in \mathbb{S}_U \cup \mathbb{S}_D, \theta(S')=1 \}|}{|\mathbb{S}_U \cup \mathbb{S}_D|} \] 当\(S'\)有任意一条port-level的边是异常时，\(\theta(S')=1\)。

    • 然后计算service \(\to\) call的权重。对于任意一个call节点\(C=S_{caller} \to S_{callee}\)，有两条service \(\to\) call类型的边：\(S_{caller} \to C\) 和 \(C \to S_{callee}\)。这两条边的权重分别为：\(\omega_{caller}\) 和 \(\omega_{callee}\)，分别计算如下： \[ \omega_{caller}=max(0, \Delta \eta)*[0.5+\beta sgn(\Delta \alpha)] \]

    \[ \omega_{callee}=max(0, \Delta \eta)*[0.5-\beta sgn(\Delta \alpha)] \] 其中，\(\Delta \alpha = \alpha(S_{caller})-\alpha(S_{callee})\)，\(\Delta \eta\)即当前服务的所有入边的权重-所有出边的权重。

异构随机游走

与Personal pageRank不同的是，作者没有用个性化向量来跳出陷阱，而是在图上加了以下几种边来防止掉入陷阱：

  • backward edge：如果有节点只有一条有向边连接，那么则加一个与有向边方向相反的backward edge，权重是有向边的\(\rho\)倍。
  • self-loop edge：给每个节点加上自环边

游走算法如下图所示，与普通的随机游走没有太大差别：

总结

  • 创新点：这篇文章的创新点不是很突出，随机游走感觉已经玩烂了（如果随机游走上能再精进一下，可能会好一些）。。。但是异构图的构建还是让人耳目一新的
  • 动机：动机比较简单，没有实证分析（对腾讯数据的实证分析应该加上的）。
  • 代码复现：公布的代码里应该是没有完整数据的，其实除公司以外的测试数据集应该要公开的。

参考文献

[1] Guo X, Peng X, Wang H, et al. Graph-based trace analysis for microservice architecture understanding and problem diagnosis, ESEC/FSE. 2020: 1387-1397. https://taoxiease.github.io/publications/esecfse20in-trace.pdf