题目:TraStrainer: Adaptive Sampling for Distributed Traces with System Runtime State
来源:FSE 2024
作者:中山大学DDS实验室
摘要
微服务系统每天都会产生大量的trace数据,带来了极大的计算和存储成本。trace sampling 技术被用来缓解这种压力。trace sampling 分为两种:
random sampling:又称 head sampling,即以固定概率决定每条trace是否采样biased sampling:又称 tail sampling,即根据trace的状态决定是否采样
很明显,random sampling
实现起来简单,但无法保证得到高质量的采样数据;biased sampling
能够根据用户偏好进行采样(比如高延时、异常状态码)。
先前的 biased sampling
工作大多基于密度(diversity),即偏好采样那些少见(edge-case)的traces,常见(common-case)的traces则少采样一些。然而,作者认为仅根据trace的状态进行采样是不充分的,应该再考虑当前系统运行状态(system
runtime
state),特别是系统处在故障状态时。(作者很有想法,在trace采样中玩了多模态,引入了metric,我觉得陈鹏飞老师实验室的工作还是很扎实且新颖的)
本文提出了TraStrainer,从以下角度进行在线采样: - 考虑密度:采用一种可解释的编码方式将trace转化为向量,方便后续密度采样 - 考虑系统状态:结合当前系统各种运行指标生成偏好向量,方便后续系统采样 - 密度采样+系统采样 \(\to\) 最终采样决策
动机
陈鹏飞老师实验室有大量关于微服务系统的故障诊断的工作,其中有许多是基于trace进行分析的,比如MicroRank,TraceRank和MicroSketch。
trace采样是这些工作的上游任务,先前与biased sampling相关的工作都是基于密度的,目标是采样edge-case
traces,没有考虑过采样的traces对下游故障诊断工作的影响。作者从以下两点进行了分析:
仅考虑edge-case traces是不够的。作者在此举例说明 common-case traces也有很大的用处:
- common-case traces 可能与根因有关。比如线程池因为太多请求的到来而用尽,而这些与根因相关的请求的traces并不一定是异常的,也就被认定为common-case traces。而我们分析这些common-case traces,可以发现这个时刻有高峰流量(这个是我根据自己理解加的)。
- common-case traces 有利于下游的分析任务。很多工作比如TraceRCA,T-Rank,都需要common-case traces来获得系统的正常模式,从而与故障时刻进行比对。
结合 system runtime state 有利于判断有价值的trace。作者拿了华为的一个真实场景进行分析,如Fig. 3所示,[a,b]时间段 Node A 的 MySQL服务进行全表查询,导致 Node A 的CPU被打满,到达 Node A 的请求变得异常。SREs通常先检查系统状态,发现CPU升高,然后分析经过 Node A 的traces。然而,如果只根据密度进行trace采样,那么[a,b]的traces将被采集的很少,因为还没有发生异常。如果结合系统状态进行采样,那么[a,b]的traces将给予更高的采样权重([a,b]存在CPU攀升)。
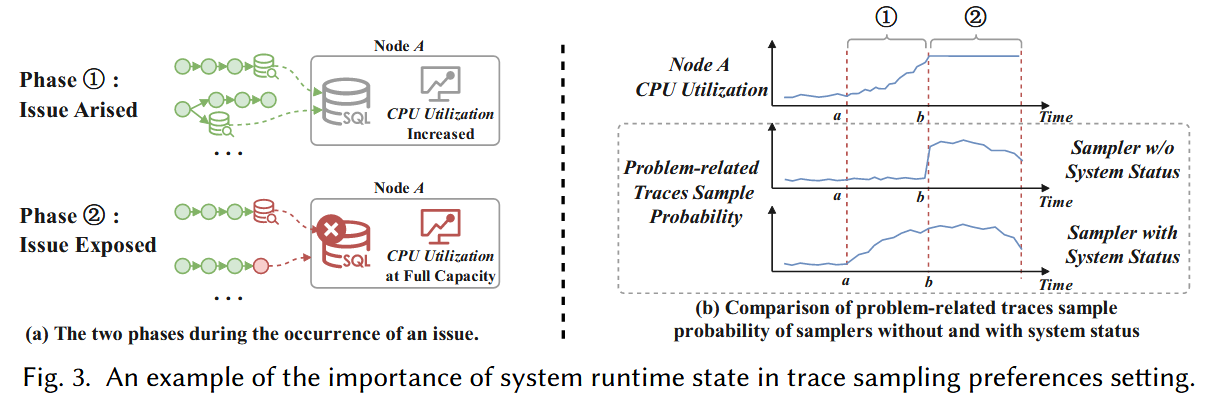
综上,作者认为应该在trace采样时不仅仅考虑traces之间的密度,也要引入对当前系统状态的考虑。
问题定义
给定一段时间收集的traces \(\mathcal{T}\)、对应的系统状态指标 \(\mathcal{M}\)、采样率 \(\beta\),需要对\(\mathcal{T}\)中每个trace \(t\) 计算采样概率 \(\rho\)。整个过程定义为:
\[ S_p(\beta, \mathcal{T}, \mathcal{M}, t) \to \rho, \mathcal{T'} \]
其中,\(\mathcal{T'}\)是\(\mathcal{T}\)的采样子集。
TraStrainer 概要
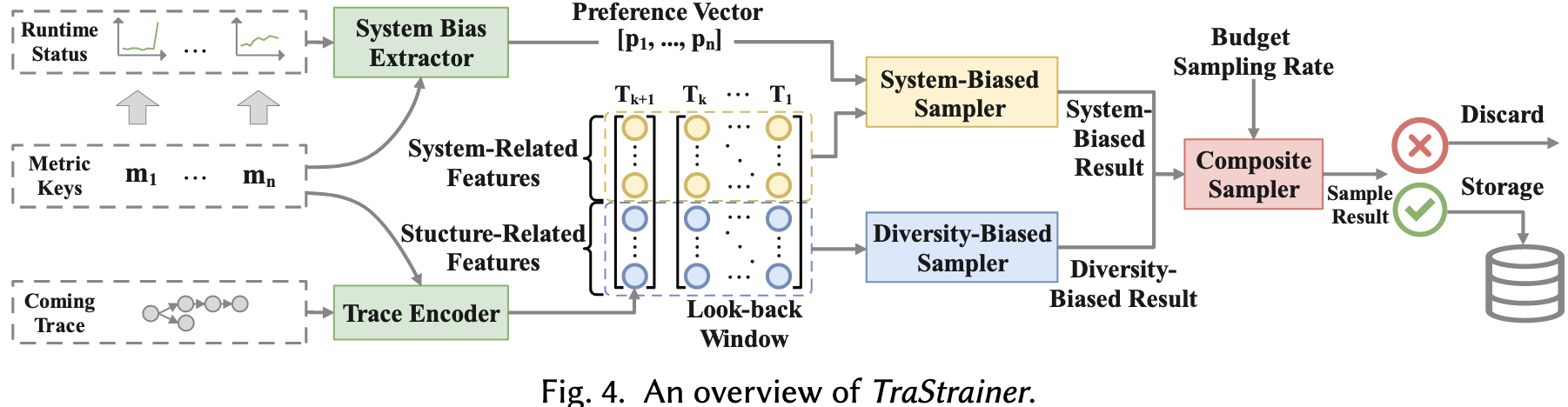
TraStrainer的架构和其他在线采样器相似,包含以下模块:
Runtime Data Preprocessing:
- Trace Encoder:对trace进行结构和状态编码
- System Bias Extractor:将当前系统状态指标进行编码
Comprehensive Sampling:
- System-Biased Sampler:优先采样与当前系统波动最相似的trace
- Diversity-Biased Sampler:优先采样edge cases traces
- Composite Sampler:结合上述两种采样器进行最终决策
Trace Encoder
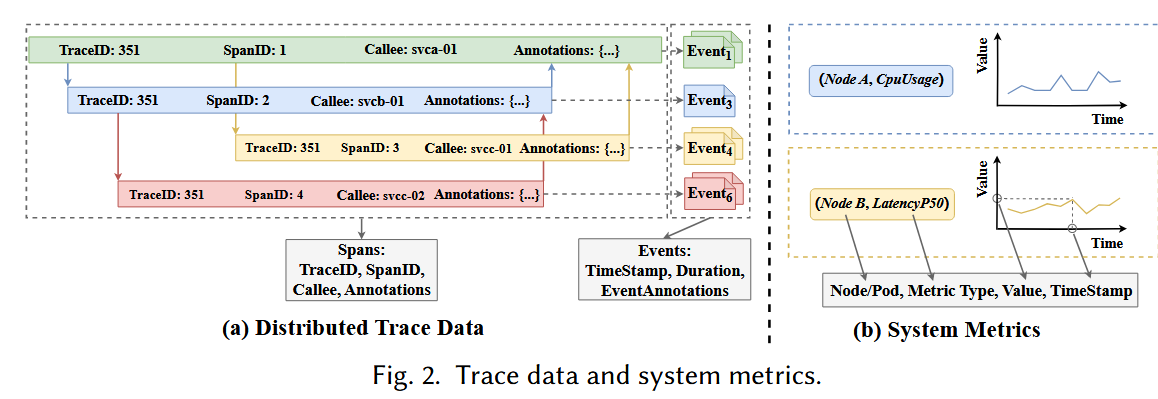
如Fig.5所示,trace的编码包含结构编码和状态编码两部分:
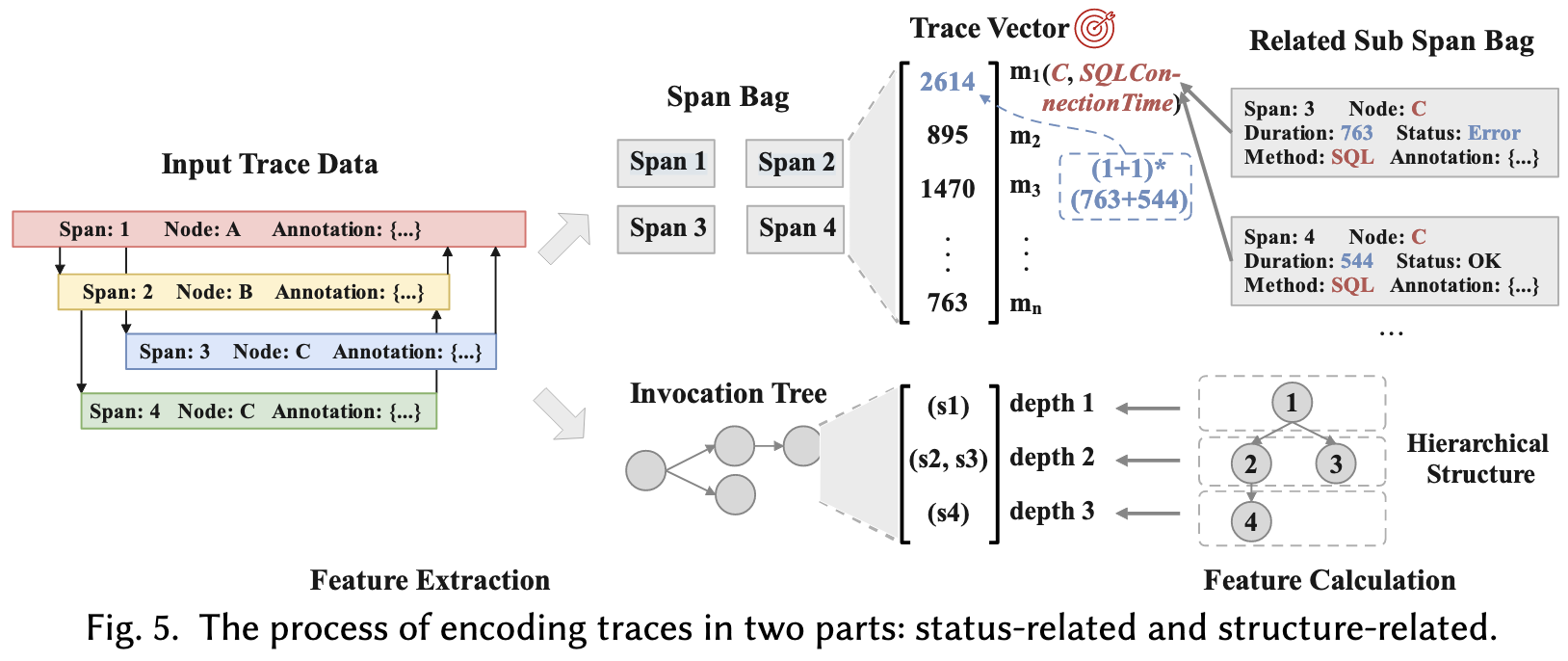
状态编码:结合 Fig. 5 的例子进行说明,Fig. 5 的Trace Vector的上半部分展示了由指标(node,metric_name)构成的向量,比如指标\(m_1\)就是(\(C\), \(SQLConnectionTime\))。一条trace由各种span构成,文章的span携带了一些tag(比如Node和annotation)。为了计算\(m_1\)的值\(f_{m_1}\),作者将所有与\(m_1\)相关的span的duration结合起来,具体计算如下:
\[ f_{m_1}=(|S_a|+1)*\sum_{i=1}^{n}s_{m_1i}.duration \]
\(s_{m_1i}\)即与指标\(m_1\)相关的span,而\(|S_a|\)即相关span中异常span的个数(状态码为error,Fig.5中为1) > 注:最开始不太理解这种设计,后来发现是作者将指标与对应的trace的状态信息(延时+状态码)联系起来,相当于量化了指标对trace状态的影响,非常巧妙。
结构编码:这一块比较简单,即将trace看做一棵树,每层可能有多个span,这些spans由parentSpan、method以及params组成,每一层的spans都被编码为一个特征。这些特征共同组成一个vector。
System Bias Extractor
这一部分的本质是衡量当前系统哪个指标比较重要,这个重要程度由指标的异常程度决定。每个指标的异常程度组合成一个一维的preference vector数组,
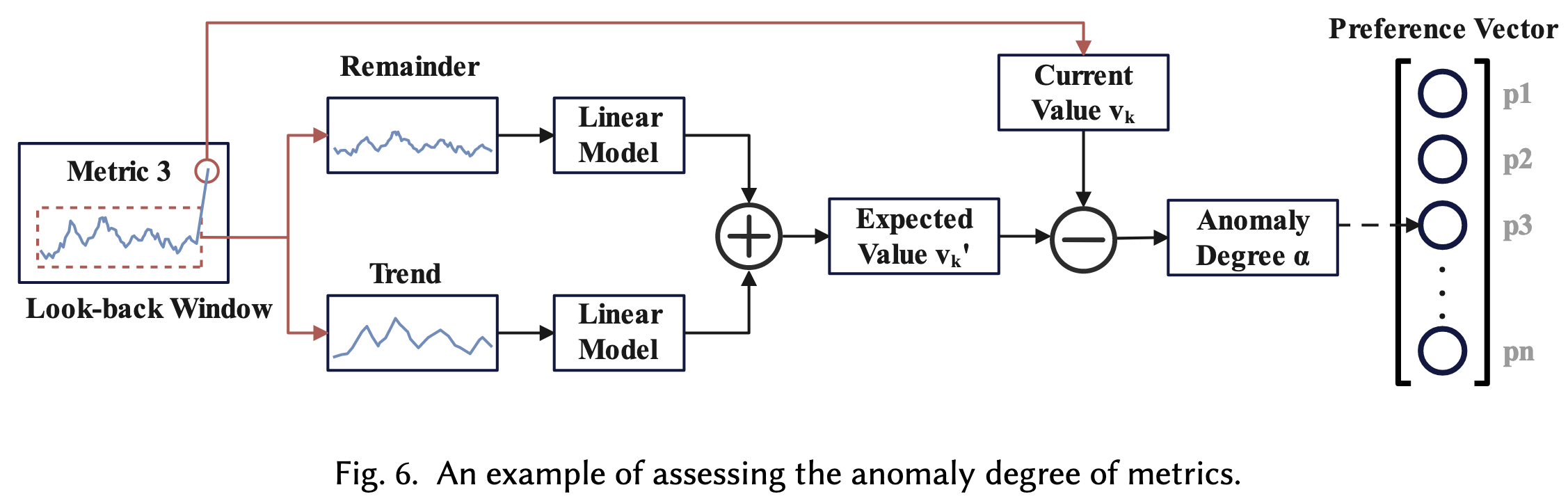
作者认为基于统计模型的异常检测不准确,无法识别周期性;而基于LSTM和Transformer的深度学习模型在响应太慢,无法适应线上采样。所以最终采用DLinear algorithm1,如Fig.6所示,这个算法通过指标的历史时序数据预测当前值\(v_k'\),并通过以下公式计算指标异常程度:
\[
\alpha=\frac{v_k'-v_k}{max(v_k', v_k)}
\]
这个公式通过预测值与真实值的差距计算异常度。所有指标\(\mathcal{M}\)的异常度拼在一起就是preference vector
\(\mathcal{P}\)。
System-Biased Sampler
System-Biased Sampler的核心是优先考虑与当前系统指标波动最相似的traces(与motivation中的故障诊断对上)。那么需要对新到来的trace进行注意力评估和采样概率计算。
本文定义了一个固定长度look-back window,由\(k\)条最近收集的历史traces组成:\([t_1,...,t_k]\)。System-Biased Sampler只需用到trace的状态编码部分,每条trace的状态向量由n个指标组成,表示为\(t_i=[f_{1i},...,f_{ni}]\)。对历史traces每一维指标计算均值\(\mu_i\)和标准差\(\sigma_i\),则对新到来的trace \(t_{k+1}\) 的第\(i\)个指标注意力分数计算如下: \[ a_i = \frac{|f_{ik+1}-\mu_i|}{\sigma_i} \]
\(t_{k+1}\)的所有指标的注意力分数记为 \(\mathcal{A}=[a_1,...,a_n]\),TraStrainer通过将注意力分数\(\mathcal{A}\)和preference vector
\(\mathcal{P}\)
进行点积得到面向系统的采样概率\(p_s\):
\[
p_s(t_{k+1})= \frac{2}{1+e^{-2\mathcal{P·\mathcal{A}(t_{k+1})}}}-1
\]
以上操作是将点积\(P·\mathcal{A}(t_{k+1})\)通过tanh函数映射到[0,1]范围,点积越大,代表当前trace与当前系统状态越相似,面向系统的采样概率越大。
Diversity-Biased Sampler
Diversity-Biased Sampler的目标是考虑edge-case traces(即少见的traces),这篇文章与先前工作一样基于聚类来筛选edge-case traces。
论文将look-back window的历史traces进行聚类(基于trace的特征),并计算每个类的质量(traces数量),并把新trace \(t_{k+1}\) 归于最近的类 \(c_{k+1}'\)。\(c_{k+1}'\)的质量为\(ma_{k+1}'\),计算 trace \(t_{k+1}\) 和 所属类\(c_{k+1}'\) 之间的Jaccard相似度\(si(t_{k+1})\)。
一般来说,所属类\(c_{k+1}'\)的质量和\(si(t_{k+1})\)越小,代表所属类越稀有、新trace越独特,应该给予更高的采样概率。所以面向密度的采样概率\(p_d(t_{k+1})\)计算如下: \[ p_d(t_{k+1})=\frac{\frac{1}{ma_{k+1}'*si(t_{k+1})}}{\sum_{i=1}^{k+1}\frac{1}{ma_{i}'*si(t_{i})}} \]
Composite Sampler
对于新到trace \(t\),综合两个采样概率 \(p_s(t)\) 和 \(p_d(t)\) 后,考虑采样额度 \(\beta\),基于动态投票机制(dynamic voting mechanism)最终决策。
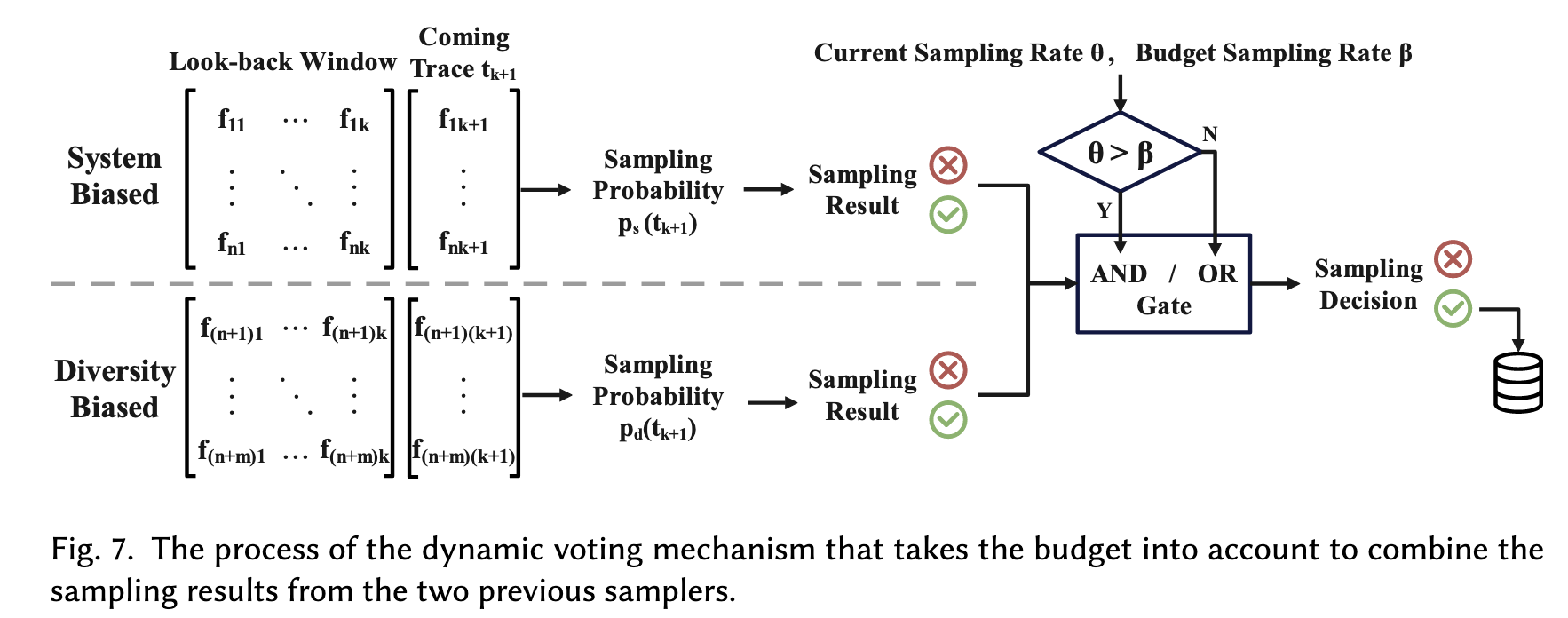
首先统计过去look-back window里采样概率 \(\theta\),如果: - \(\theta \geq \beta\),必须两个采样决策都为True,才采样 - \(\theta \leq \beta\),只需要有一个采样决策为True,即可采样