期望最大算法（Expectation Maximization Algorithm）

介绍

期望最大化算法（Expectation-Maximization algorithm, EM）是一种在统计学中估计概率模型参数的方法，特别适用于包含隐变量（latent variables）的概率模型。

如果一个概率模型只有观测变量，那么我们可以基于观测得到的数据，用最大似然估计求得概率模型的参数。但是如果概率模型还包含了无法观测的变量（隐变量），则无法用上述方法估计，所以需要考虑隐变量，引入新的方法对参数进行估计。

应用举例

假设我们有一组一维数据\(X=\{x_1, x_2,...,x_n\}\)，我们认为这些数据是由2个正态分布混合而成的。我们的目标是估计这2个正态分布的参数（均值和方差）以及它们各自的权重。参数如下：

• 第1个分布 \(N(\mu_1, \sigma_1)\)，其中\(\mu_1=5\), \(\sigma_1=9\)
• 第2个分布 \(N(\mu_2, \sigma_2)\)，其中\(\mu_2=15\), \(\sigma_2=0.5\)

两个分布的权重满足：\(\sum_{k=1}^2\pi_k=1\)

我们目前手中只有这一组一维观测数据\(X=\{x_1, x_2,...,x_n\}\)，已知观测数据由2个正态分布组成，目标是求出这2个正态分布的参数以及各自的权重。

注意，我们不能直接使用观测数据去拟合2个分布，因为观测数据的分布实际上是2个正态分布混合而成，其中包含了一个隐变量：

\[ z_i= \begin{cases} 0& x_i \in N(\mu_1, \sigma_1^2)\\ 1& x_i \in N(\mu_2, \sigma_2^2) \end{cases} \]

隐变量\(z_i\)表示数据点\(x_i\)由哪个分布生成。而隐变量\(z_i\)的值无法被观测，所以当我们用最大似然估计去做时，需要考虑所有可能的隐变量情况（不同取值的权重）：

\[ \begin{aligned} L(\theta)&=\prod_{i=1}^{n}f(x_i;\theta) \\ ln L(\theta) &= \sum_{i=1}^{n}ln f(x_i:\theta) \\ &= \sum_{i=1}^{n}ln \sum_{k=1}^{2} \pi_k f(x_i:\theta_k) \end{aligned} \] 但由于 \(\pi_k\)未知，所以难以进行最大似然估计。

EM算法步骤

我们首先用两个正态分布混合生成观测数据：

np.random.seed(8)
n_samples = ⅓
data = np.concatenate((np.random.normal(5, 3, n_samples),
                       np.random.normal(15, 0.5, n_samples)))

并随机给予两个分布初始参数以及权重，代码如下：

mu1, sigma1 = 10, 1
mu2, sigma2 = 20, 1
pi1, pi2 = 0.5, 0.5

tolerance = 1e-6
max_iterations = 1000

EM算法分为两个步骤： ### E步（期望步, Expectation step）： 我们需要计算每个数据点 \(x_i\) 属于不同分布的后验概率（本质上是隐变量z的条件期望值），此处可以使用贝叶斯公式计算得到：

\[ \begin{aligned} P(z_i=1|x_i, \theta)&=\frac{P(x_i|z_i=1)P(z_i=1)}{P(x_i)}=\frac{P(x_i|z_i=1)P(z_i=1)}{P(x_i|z_i=1)P(z_i=1)+P(x_i|z_i=2)P(z_i=2)}\\ &=\frac{\pi_1N(x_i|\mu_1, \sigma_1^2)}{\pi_1N(x_i|\mu_1, \sigma_1^2) + \pi_2N(x_i|\mu_2, \sigma_2^2)} \end{aligned} \]

同理可以求得\(P(z_i=2|x_i, \theta)\)。代码如下：

def normal_pdf(x, mu, sigma):
    # 计算x_i的概率密度
    return (1 / (np.sqrt(2 * np.pi) * sigma)) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)

for iteration in range(max_iterations):
    # E步：计算后验概率
    likelihood1 = normal_pdf(data, mu1, sigma1)
    likelihood2 = normal_pdf(data, mu2, sigma2)
    total_likelihood = pi1 * likelihood1 + pi2 * likelihood2
    posterior1 = (pi1 * likelihood1) / total_likelihood
    posterior2 = (pi2 * likelihood2) / total_likelihood

M步（最大化步, Maximization step）：

在E步得到 \(x_i\) 属于不同分布的后验概率后，也是隐变量\(z_i\)的条件期望后，我们利用这个期望来更新参数估计值，以最大化观测数据的似然函数。

因为现在已经知道了关于隐变量z_i的条件期望，所以我们可以用最大似然估计去估计各分布的参数了：

\[ \mu_k=\mathop{\arg\max}\limits_{\mu_k}{\sum_{i=1}^{n}P(z_i=k|x_i, \theta)}lnf(x_i;\mu_k,\sigma_k^2) \]

\[ \sigma_k^2=\mathop{\arg\max}\limits_{\sigma_k^2}{\sum_{i=1}^{n}P(z_i=k|x_i, \theta)}lnf(x_i;\mu_k,\sigma_k^2) \]

对上述两式进行求解可得各部分更新公式如下（\(\pi_k\)更新同理）： \[ \mu_k = \frac{\sum_{i=1}^{n}P(z_i=k|x_i,\theta)x_i}{\sum_{i=1}^{n}P(z_i=k|x_i,\theta)} \]

\[ \sigma_k^2 = \frac{\sum_{i=1}^{n}P(z_i=k|x_i, \theta)(x_i-\mu_k)^2}{\sum_{i=1}^{n}P(z_i=k|x_i,\theta)} \]

\[ \pi_k=\frac{1}{n}\sum_{i=1}^{n}P(z_i=k|x_i,\theta) \]

代码如下：

# M步: 更新参数
pi1_new = np.mean(posterior1)
pi2_new = np.mean(posterior2)
mu1_new = np.sum(posterior1 * data) / np.sum(posterior1)
mu2_new = np.sum(posterior2 * data) / np.sum(posterior2)
sigma1_new = np.sqrt(np.sum(posterior1 * (data - mu1_new) ** 2) / np.sum(posterior1))
sigma2_new = np.sqrt(np.sum(posterior2 * (data - mu2_new) ** 2) / np.sum(posterior2))

完整代码如下：

import numpy as np
import matplotlib.pyplot as plt

# 生成数据
np.random.seed(8)
n_samples = 100
data = np.concatenate((np.random.normal(5, 3, n_samples // 2),
                       np.random.normal(15, 0.5, n_samples // 2)))

# 初始化参数
mu1, sigma1 = 10, 1
mu2, sigma2 = 20, 1
pi1, pi2 = 0.5, 0.5
tolerance = 1e-6
max_iterations = 1000

def normal_pdf(x, mu, sigma):
    return (1 / (np.sqrt(2 * np.pi) * sigma)) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)

for iteration in range(max_iterations):
    # E步: 计算后验概率
    likelihood1 = normal_pdf(data, mu1, sigma1)
    likelihood2 = normal_pdf(data, mu2, sigma2)
    total_likelihood = pi1 * likelihood1 + pi2 * likelihood2
    posterior1 = (pi1 * likelihood1) / total_likelihood
    posterior2 = (pi2 * likelihood2) / total_likelihood
    
    # M步: 更新参数
    pi1_new = np.mean(posterior1)
    pi2_new = np.mean(posterior2)
    mu1_new = np.sum(posterior1 * data) / np.sum(posterior1)
    mu2_new = np.sum(posterior2 * data) / np.sum(posterior2)
    sigma1_new = np.sqrt(np.sum(posterior1 * (data - mu1_new) ** 2) / np.sum(posterior1))
    sigma2_new = np.sqrt(np.sum(posterior2 * (data - mu2_new) ** 2) / np.sum(posterior2))

    # 检查是否收敛
    if (abs(mu1_new - mu1) < tolerance and
        abs(mu2_new - mu2) < tolerance and
        abs(sigma1_new - sigma1) < tolerance and
        abs(sigma2_new - sigma2) < tolerance):
        break

    # 更新参数
    mu1, mu2, sigma1, sigma2, pi1, pi2 = mu1_new, mu2_new, sigma1_new, sigma2_new, pi1_new, pi2_new

# 打印最终结果
print(f"迭代次数: {iteration}")
print(f"μ1: {mu1}, σ1: {sigma1}, π1: {pi1}")
print(f"μ2: {mu2}, σ2: {sigma2}, π2: {pi2}")

# 绘制结果
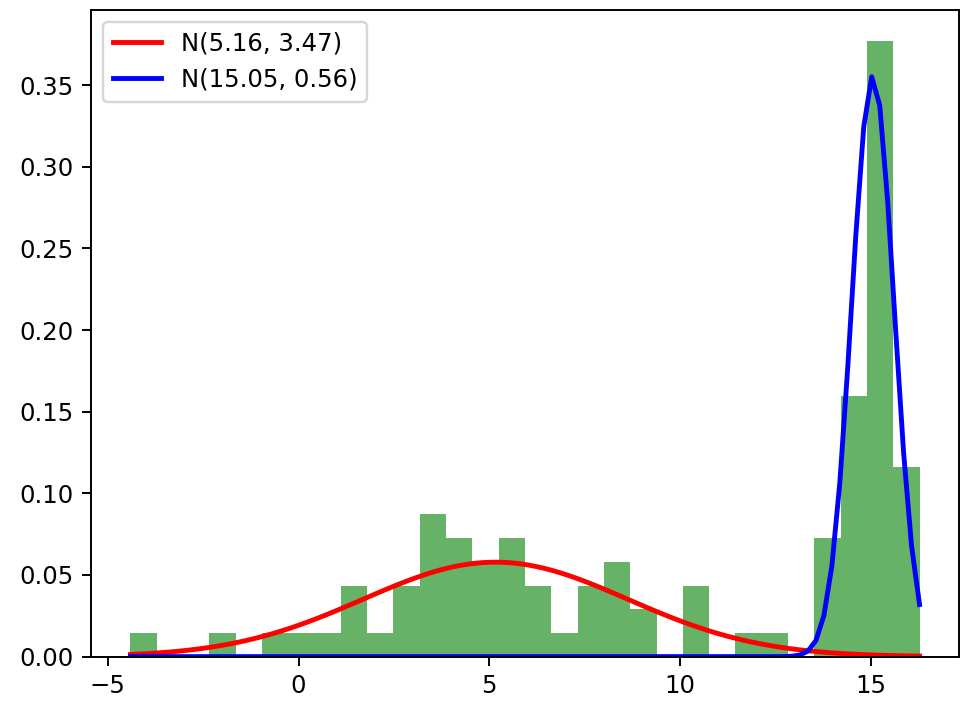
plt.hist(data, bins=30, density=True, alpha=0.6, color='g')
x = np.linspace(min(data), max(data), 100)
plt.plot(x, pi1 * normal_pdf(x, mu1, sigma1), 'r-', lw=2, label=f'N({mu1:.2f}, {sigma1:.2f})')
plt.plot(x, pi2 * normal_pdf(x, mu2, sigma2), 'b-', lw=2, label=f'N({mu2:.2f}, {sigma2:.2f})')
plt.legend()
plt.show()

结果输出如下：